Gentle Intro to Linear Algebra - 0

What is mathematics about? I am not qualified to answer this, but I will anyway (remember, a fistful of salt on everything here). To me, mathematics is the extraction and study of structure.

Consider the set of integers (both positive and negative) denoted $\mathbb{Z}$. The set of integers is a thing. As a set alone it's just a bag of stuff. There is nothing wrong in saying $\mathbb{Z}=\{-500,1,2000,30,7,53,\dots \}$ but it feels off. That's because when we're thinking about integers, we're thinking about many things: Order (a notion of one element being smaller or larger than another), addition, subtraction, multiplication, divisibility, and so on.

So our notion of integers is not just a collection of things, but it has structure. It has ordering, and operations defined on it, all with their own properties.

Then, how much of what makes integers, integers comes from its structure? And how much of it comes from it as a thing: a set alone? And if we were to keep the structure part of the integers intact, and replace the thing part, would we still preserve its essence?

The answer is yes to the last question, not just for integers, but for many other things in mathematics.

You can call this process generalisation or abstraction or whatever you want. But let's get a concrete example going. I will throw this sentence out there, and if it makes you uncomfortable, don't worry. We will get there. Here goes:
A vector is an element of a vector space.
Yeah, not an arrow, not a list of real numbers, not a column matrix, not something with magnitude and direction. Although all these are representations that are extremely useful, and are contextually correct (even mathematically correct as a special case of a more general object). Maybe the arrow idea goes well with physics, a list of real numbers/column matrix goes well with machine learning, and so on...

Mass, velocity, momentum:

We know that mass is a scalar, meaning that one real number is sufficient to describe the mass of an object.
We say velocity is a vector because it has magnitude and direction, which compels us to think about a vector as an arrow.
When you look at the equation $\mathbf{p}=m\mathbf{v}$ (I'll use bold letters for vectors), you might think of the velocity vector $\mathbf{v}$ as an arrow pointing in the direction that the particle is moving right now, and the length of the arrow tells you how "fast" it is. And then, you think about the mass of this particle scaling that velocity arrow's length to give you the momentum vector $\mathbf{p}$.

This is a very reasonable and intuitive understanding of vectors. But as math people, we don't shy away from abstraction. So let us extract the first bit of structure from our discussion on momentum: (note sp stands for structural property)

sp-1: A vector can be multiplied by a scalar resulting in another vector in the same space and in the same direction. That is: $\lambda$ is a scalar and $\mathbf{v}$ is a vector, then $\lambda \mathbf{v}$ is a vector, in the same as $\mathbf{v}$.

Note: we will use these sps to actually define vectors and scalars and directions later (this is not circular because everything so far is an informal discussion).

Why does sp-1 make sense? Well, if you take an arrow that you drew on a piece of paper, and extend/shorten it within that piece of paper, it is still an arrow, and it still lives on that piece of paper, and is still pointing in the same direction as the initial arrow that we drew.

Forces

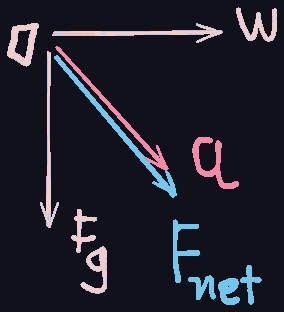
Imagine a light piece of paper falling under the influence of a very heavy horizontal wind. For simplicity's sake, assume that the wind force vector $\mathbf{w}$ is completely horizontal, and the gravitational force ${\mathbf{F}}_{\mathbf{g}}$ is of course pointing downwards.

Dropping the famous $\mathbf{F}=m\mathbf{a}$, we know that the acceleration of this paper will be in the direction of the "net" or "total" resultant force. Intuitively, we know that the paper will move down and to the right. So this must mean that the resulting force ${\mathbf{F}}_{\mathbf{net}}$ will point down and to the right.
So there is a notion of adding vectors:
${\mathbf{F}}_{\mathbf{net}}={\mathbf{F}}_{\mathbf{g}}{+}_v\mathbf{w}$
and in our "arrow" viewpoint of vectors, the again famous parallelogram law will tell you that to get ${\mathbf{F}}_{\mathbf{net}}$, you can join the head of ${\mathbf{F}}_{\mathbf{g}}$ with the tail of $\mathbf{w}$, or vice versa. This means that the order of doing addition does not matter (commutative). Moreover, joining two arrows results in an arrow in the same space. (note that ${+}_v$ indicates that this addition is between two vectors)

Finally, if you chain three vectors as arrows, each tail starting at the head of the previous one, it doesn't matter in what order you chain them, you will still end up at the same place (associative).

Now, what structure can we extract from this? We don't want to extract anything that is strict with the arrow viewpoint, so in general we have the following:

sp-2: Two (or more) vectors can be added, resulting in another vector in the same space. Moreover, this addition is commutative: that is, $\mathbf{u}{+}_v\mathbf{v}=\mathbf{v}{+}_v\mathbf{u}$, and associative:
$\mathbf{u}{+}_v(\mathbf{v}{+}_v\mathbf{w})=(\mathbf{u}{+}_v\mathbf{v}){+}_v\mathbf{w}$
(it doesn't matter where you put the brackets or which addition you resolve first).

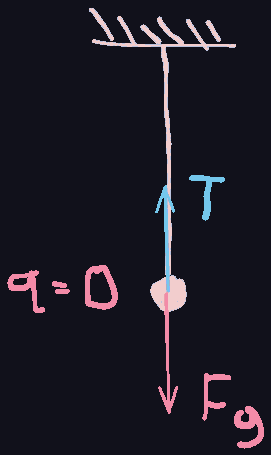
Okay, now imagine a bob hanging by a taut string. The tension on the rope is pulling it up, and gravity is pulling it down, and yet the bob remains still. So that must mean that the resulting force is a zero vector, denoted $\mathbf{0}$. Moreover, it also must mean that any arrow can be zeroed out by adding an equal and opposite arrow to it!

Moreover, this zero vector does nothing when added to any other vector. (Imagine a "non-existent" arrow joined to the head of another arrow.)

sp-3: There is a zero vector that acts as an additive identity, meaning that upon addition to any vector, it preserves that vector. That is, $\mathbf{v}{+}_v\mathbf{0}=\mathbf{v}$. Moreover, every vector has its equal and opposite vector: its additive inverse. When a vector is added to its additive inverse, you get the zero vector:
$\mathbf{v}{+}_v(-\mathbf{v})=\mathbf{0}$
(note that $-\mathbf{v}$ is just notation for the additive inverse of $\mathbf{v}$).

Distributive laws:

Now, imagine taking two arrows, and doubling their length, and then adding them up. Then imagine first adding the two arrows and then doubling the length of the result.
They both result in the same thing. (Use your geometric intuition to convince yourself that this is true, apologies for the bad parallelograms).

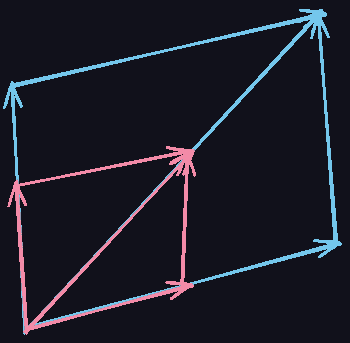
Notice that the blue arrows are double the pink ones in length, and the pink diagonal vector lands halfway on the blue diagonal vector.
Therefore, adding the two pink vectors first and then doubling its length results in the blue diagonal vector.

So we get our first distributive law!

sp-4: Scalar multiplication distributes over vector addition. That is:
$\lambda (\mathbf{u}{+}_v\mathbf{v})=\lambda \mathbf{u}{+}_v\lambda \mathbf{v}$
(You can add two arrows, then scale them — or you can scale each arrow by the same amount, then add them. It's all the same.)

Naturally, one can add two scalars too. (For now, think about scalars as just real numbers.) So then, is it true that adding two scalars and then scaling a vector by that amount is the same as scaling a vector by the first scalar, then by the second scalar, and adding the two resulting vectors? The answer is again yes.

Take a single vector (brown) and scale it by two amounts (pink, blue) and join them. Effectively all you've done is scale the brown vector by an amount equal to the sum of the lengths of the pink and blue vectors (white vector).

We get our second distributive law.

sp-5: Vectors distribute over scalar addition. That is:
$(\lambda +\mu )\mathbf{v}=\lambda \mathbf{v}{+}_v\mu \mathbf{v}$
(Notice that the addition on the left is between two scalars, and on the right it's between two vectors.)

So far, we have almost pretended like scalars can only be positive. But of course, they can be negative too. Intuitively, a negative scalar should rotate a vector by 180 degrees, and the magnitude of that scalar will change the length of the vector.

sp-6: With this, we notice that the scalar $1$ leaves a vector unchanged on scalar multiplication, and a scalar of $-1$ produces the additive inverse (equal in length and opposite in direction) of a vector upon scalar multiplication.
i.e. $1\mathbf{v}=\mathbf{v}$ and $-1\mathbf{v}=-\mathbf{v}$.

Finally, we know that scalars can be multiplied among themselves as well. If you double the length of an arrow and then triple it, effectively, you've just scaled its length by six times.

sp-7 Scaling a vector by a scalar equal to the product of two scalars, is the same thing as scaling it by one, and then by the other. That is, $(\lambda \cdot \mu )\mathbf{v}=\lambda (\mu \mathbf{v})$ (On the right hand, we are doing two scalar-vector multiplications, one after the other. on the left, the two scalars are multiplied together first, and we do one scalar - vector multiplication).

So far, we have collected 7 informal structural properties of vectors. Now, you might think that these properties are pedantic, obvious, or even unnecessary in the amount of detail we've added to it. However, vectors don't have to be arrows, they just have to behave like arrows, and scalars don't have to be real numbers, they just have to behave like real numbers. We get to choose what a vector is, and we get to define addition on vectors, we get to choose our scalars, define scalar-vector multiplication ... and as long as we adhere to structural properties, our intuition from arrows or any other representation of your choice will still apply.
A function can be a vector, a polynomial can be a vector. A function between vectors can be a vector!!

Therefore, we have a lot of freedom, and with freedom comes great power, and with great power comes great responsibility. Our great responsibility is to pay attention to the detail in the structure that we are extracting, so that we can then create well defined mathematical objects.