2 - Vectors

Informally, a vector is resented as an arrow, or points in ${\mathbb{R}}^n$ or ${\mathbb{C}}^n$, which are written as column vectors $$\vec{x} = \begin{bmatrix}x_{1}\x_{2}\ \vdots \x_{n}\end{bmatrix}$$ Where $x_i\in \mathbb{R}$ or $x_i\in \mathbb{C}$. for short hand, we may write $\overrightarrow{x}=[x_i{]}_n$.
If we have two vectors $\overrightarrow{x}=[x_i{]}_n,\overrightarrow{y}=[y_i{]}_n$, then $\overrightarrow{x}+\overrightarrow{y}=[x_i+y_i{]}_n$. Geometrically, if we have two arrows, for $\overrightarrow{x},\overrightarrow{y}$. Then, one can equivalently either put a copy of $\overrightarrow{x}$ with the tail at the head of $\overrightarrow{y}$ or put a copy of $\overrightarrow{y}$ with the tail at the head of $\overrightarrow{x}$.

One can also change the length of the vector using a positive scalar, shortening it if the scalar is smaller than one, otherwise making it longer. if the scalar is negative, the scaled vector points opposite to the original.
$a\overrightarrow{x}=[a{x}_i{]}_n$ where $a\in \mathbb{R}$.

Dot product:

if $\overrightarrow{x},\overrightarrow{y}\in {\mathbb{R}}^n$, then the dot product $\overrightarrow{x}\cdot \overrightarrow{y}:=\sum _{i=1}^n{x}_i{y}_i\in \mathbb{R}$. The same thing holds for dot products of vectors in ${\mathbb{C}}^n$.
Geometrically, think law of cosines:

<ns0:svg xmlns:ns0="http://www.w3.org/2000/svg" x="0" y="0" width="661.45458984375" height="459.90911865234375" style=" width:661.45458984375px; height:459.90911865234375px; background: transparent; fill: none; "> <ns0:svg class="role-diagram-draw-area"><ns0:g class="shapes-region" style="stroke: black; fill: none;"><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M100,302 L591.88,392.01" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.9836658555866438,-0.18000412371108662,0.18000412371108662,-0.9836658555866438,595.8181762695311,392.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M100,302 L405.8,35.36" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.7536781144482301,0.6572437141591851,-0.6572437141591851,-0.7536781144482301,408.81817626953125,32.727272033691406)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M595.82,392.73 L410.66,36.28" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(0.4609743745354622,0.8874134470592834,-0.8874134470592834,0.4609743745354622,408.81817626953125,32.727272033691406)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M149.82,312.73 C164.37,295.27 146.93,279.69 128.53,276.94" style="stroke: rgb(0, 0, 0); stroke-width: 1; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(0.9945036365624706,0.10470203849028566,-0.10470203849028566,0.9945036365624706,126.81817626953125,276.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 1;"><ns0:path d=" M10.93,-3.29 Q4.96,-0.45 0,0 Q4.96,0.45 10.93,3.29" /></ns0:g></ns0:g><ns0:g /></ns0:g><ns0:g /><ns0:g /><ns0:g /></ns0:svg> <ns0:svg width="660" height="458.4545593261719" style="width:660px;height:458.4545593261719px;font-family:Asana-Math, Asana;background:transparent;">ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,243.20458984375,130.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M271 204L242 77C238 60 236 42 236 26C236 4 245 -9 260 -9C283 -9 324 17 406 85L399 106C375 86 346 59 324 59C315 59 309 68 309 82C309 87 309 90 310 93L402 472L392 481L359 463C318 478 301 482 274 482C246 482 226 477 199 464C137 433 104 403 79 354C35 265 4 145 4 67C4 23 19 -11 38 -11C75 -11 155 41 271 204ZM319 414C297 305 278 253 244 201C187 117 126 59 94 59C82 59 76 72 76 99C76 163 104 280 139 360C163 415 186 433 234 433C257 433 275 429 319 414Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="242.727294921875" overflow="visible" y="111.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,317.04547119140625,385.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M235 722L223 733C171 707 135 698 63 691L59 670L107 670C131 670 141 663 141 646C141 639 140 628 139 622L38 71C37 68 37 64 37 61C37 22 85 -11 140 -11C177 -11 228 8 271 39C367 107 433 244 433 376C433 414 424 453 412 468C405 477 392 482 377 482C353 482 323 474 295 460C244 433 211 403 149 324ZM322 424C348 424 361 401 361 352C361 288 340 202 310 137C277 68 237 36 183 36C137 36 112 59 112 101C112 135 127 276 208 361C241 395 293 424 322 424Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="316.727294921875" overflow="visible" y="362.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,518.5227661132812,187.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M342 330L365 330C373 395 380 432 389 458C365 473 330 482 293 482C248 483 175 463 118 400C64 352 25 241 25 136C25 40 67 -11 147 -11C201 -11 249 9 304 54L354 95L346 115L331 105C259 57 221 40 186 40C130 40 101 80 101 159C101 267 136 371 185 409C206 425 230 433 261 433C306 433 342 414 342 390Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="517.727294921875" overflow="visible" y="168.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,163.727294921875,288.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M237 -16C473 -16 572 316 576 504C578 618 546 702 419 702C159 702 72 412 69 199C67 80 101 -16 237 -16ZM401 676C536 676 506 491 485 381L169 381C194 485 272 676 401 676ZM253 13C102 13 147 261 163 349L479 349C454 237 396 13 253 13Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g></ns0:svg></ns0:svg>

but, $\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}$, equivalently $$|\vec{a}- \vec{b}|^2 = |\vec{a}|^2 + |\vec{b}|^2 -2|\vec{a}||\vec{b}|\cos(\theta)$$
Then, assuming $a,b\in {\mathbb{R}}^n$ or ${\mathbb{C}}^n$, and doing a little algebra, we have that:

$\overrightarrow{a}\cdot \overrightarrow{b}$ is the length of the projection of $\overrightarrow{a}$ onto $\overrightarrow{b}$ or vice versa.
Moreover, $\overrightarrow{a}\perp \overrightarrow{b}$ if and only if $\overrightarrow{a}\cdot \overrightarrow{b}=0$.

<ns0:svg xmlns:ns0="http://www.w3.org/2000/svg" x="0" y="0" width="661.45458984375" height="459.90911865234375" style=" width:661.45458984375px; height:459.90911865234375px; background: transparent; fill: none; "> <ns0:svg class="role-diagram-draw-area"><ns0:g class="shapes-region" style="stroke: black; fill: none;"><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M100,302 L591.88,392.01" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.9836658555866438,-0.18000412371108662,0.18000412371108662,-0.9836658555866438,595.8181762695311,392.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M100,302 L405.8,35.36" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.7536781144482301,0.6572437141591851,-0.6572437141591851,-0.7536781144482301,408.81817626953125,32.727272033691406)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M149.82,312.73 C164.37,295.27 146.93,279.69 128.53,276.94" style="stroke: rgb(0, 0, 0); stroke-width: 1; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(0.9945036365624706,0.10470203849028566,-0.10470203849028566,0.9945036365624706,126.81817626953125,276.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 1;"><ns0:path d=" M10.93,-3.29 Q4.96,-0.45 0,0 Q4.96,0.45 10.93,3.29" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="3.375 4.0200000000000005" d=" M408.82,32.73 L354.82,349.73" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M100,302 L349.9,348.81" style="stroke: rgb(52, 61, 85); stroke-width: 4; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(52,61,85)" transform="matrix(-0.982903228611439,-0.1841229023918788,0.1841229023918788,-0.982903228611439,354.8181762695312,349.7272720336914)" style="stroke: rgb(52, 61, 85); stroke-width: 4;" stroke-opacity="1"><ns0:path d=" M20.77,-6.25 Q9.42,-0.85 0,0 Q9.42,0.86 20.77,6.25" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M364,350 L416.98,39.66" style="stroke: rgb(29, 34, 46); stroke-width: 4; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(29,34,46)" transform="matrix(-0.16831733928979567,0.9857328610198626,-0.9857328610198626,-0.16831733928979567,417.81817626953125,34.727272033691406)" style="stroke: rgb(29, 34, 46); stroke-width: 4;" stroke-opacity="1"><ns0:path d=" M20.77,-6.25 Q9.42,-0.85 0,0 Q9.42,0.86 20.77,6.25" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M100,302 L199.93,320.46" style="stroke: rgb(0, 0, 0); stroke-width: 5; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="none" fill="rgb(0,0,0)" fill-opacity="1" transform="matrix(-0.983381892337729,-0.18154903971728206,0.18154903971728206,-0.983381892337729,206.81817626953125,321.72727203369135)" style="stroke: none; fill: rgb(0, 0, 0); stroke-width: 5;"><ns0:path d=" M20.54,-9.87 L0,0 L20.54,9.87 Z" /></ns0:g></ns0:g><ns0:g /></ns0:g><ns0:g /><ns0:g /><ns0:g /></ns0:svg> <ns0:svg width="660" height="458.4545593261719" style="width:660px;height:458.4545593261719px;font-family:Asana-Math, Asana;background:transparent;">ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,243.20458984375,130.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M271 204L242 77C238 60 236 42 236 26C236 4 245 -9 260 -9C283 -9 324 17 406 85L399 106C375 86 346 59 324 59C315 59 309 68 309 82C309 87 309 90 310 93L402 472L392 481L359 463C318 478 301 482 274 482C246 482 226 477 199 464C137 433 104 403 79 354C35 265 4 145 4 67C4 23 19 -11 38 -11C75 -11 155 41 271 204ZM319 414C297 305 278 253 244 201C187 117 126 59 94 59C82 59 76 72 76 99C76 163 104 280 139 360C163 415 186 433 234 433C257 433 275 429 319 414Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="242.727294921875" overflow="visible" y="111.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,316.727294921875,381.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M492 473L485 482L417 465L407 414C392 336 367 268 336 221C277 130 199 59 159 59C151 59 146 68 146 85C146 99 148 112 153 137L210 408C213 424 215 438 215 451C215 470 206 482 192 482C172 482 134 461 60 408L32 388L39 368L71 389C99 407 110 412 119 412C128 412 136 403 136 392C136 388 135 378 134 374L71 77C69 68 67 44 67 30C67 7 82 -11 102 -11C165 -11 286 101 370 239L333 97C326 73 322 46 322 31C322 6 333 -9 352 -9C378 -9 414 12 512 85L502 103L476 86C452 70 426 59 415 59C407 59 402 66 402 76C402 112 477 416 492 473Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="316.727294921875" overflow="visible" y="362.7272720336914" height="10" width="10.284090995788574"><ns0:path d=" M 10.28 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 8.14 v -0.90 h -8.14 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,163.727294921875,288.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M237 -16C473 -16 572 316 576 504C578 618 546 702 419 702C159 702 72 412 69 199C67 80 101 -16 237 -16ZM401 676C536 676 506 491 485 381L169 381C194 485 272 676 401 676ZM253 13C102 13 147 261 163 349L479 349C454 237 396 13 253 13Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,299.727294921875,322.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M271 204L242 77C238 60 236 42 236 26C236 4 245 -9 260 -9C283 -9 324 17 406 85L399 106C375 86 346 59 324 59C315 59 309 68 309 82C309 87 309 90 310 93L402 472L392 481L359 463C318 478 301 482 274 482C246 482 226 477 199 464C137 433 104 403 79 354C35 265 4 145 4 67C4 23 19 -11 38 -11C75 -11 155 41 271 204ZM319 414C297 305 278 253 244 201C187 117 126 59 94 59C82 59 76 72 76 99C76 163 104 280 139 360C163 415 186 433 234 433C257 433 275 429 319 414Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g>ns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,307.7613525390625,325.7295669555664)"><ns0:path transform="matrix(0.0119,0,0,-0.0119,0,0)" d="M179.50274 -172L179.50274 713L120.50274 713L120.50274 -172ZM479.50274 -172L479.50274 713L420.50274 713L420.50274 -172Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="299.727294921875" overflow="visible" y="299.7272720336914" height="10" width="17.03409194946289"><ns0:path d=" M 17.03 5.39 l -3.50 -3.69 l -0.54 0.58 l 2.14 2.58 h -0.17 v 1.00 h 0.17 l -2.14 2.58 l 0.54 0.58 z M 1.87 5.81 h 14.65 v -1.00 h -14.65 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,429.727294921875,82.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M271 204L242 77C238 60 236 42 236 26C236 4 245 -9 260 -9C283 -9 324 17 406 85L399 106C375 86 346 59 324 59C315 59 309 68 309 82C309 87 309 90 310 93L402 472L392 481L359 463C318 478 301 482 274 482C246 482 226 477 199 464C137 433 104 403 79 354C35 265 4 145 4 67C4 23 19 -11 38 -11C75 -11 155 41 271 204ZM319 414C297 305 278 253 244 201C187 117 126 59 94 59C82 59 76 72 76 99C76 163 104 280 139 360C163 415 186 433 234 433C257 433 275 429 319 414Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g>ns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,437.76141357421875,85.72955169677735)"><ns0:path transform="matrix(0.0119,0,0,-0.0119,0,0)" d="M684 -79L684 -20L404 -20L404 621L345 621L345 -20L65 -20L65 -79Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="429.727294921875" overflow="visible" y="59.727272033691406" height="10" width="18.795455932617188"><ns0:path d=" M 18.80 5.39 l -3.50 -3.69 l -0.54 0.58 l 2.14 2.58 h -0.17 v 1.00 h 0.17 l -2.14 2.58 l 0.54 0.58 z M 1.87 5.81 h 16.42 v -1.00 h -16.42 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,162.727294921875,346.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M492 473L485 482L417 465L407 414C392 336 367 268 336 221C277 130 199 59 159 59C151 59 146 68 146 85C146 99 148 112 153 137L210 408C213 424 215 438 215 451C215 470 206 482 192 482C172 482 134 461 60 408L32 388L39 368L71 389C99 407 110 412 119 412C128 412 136 403 136 392C136 388 135 378 134 374L71 77C69 68 67 44 67 30C67 7 82 -11 102 -11C165 -11 286 101 370 239L333 97C326 73 322 46 322 31C322 6 333 -9 352 -9C378 -9 414 12 512 85L502 103L476 86C452 70 426 59 415 59C407 59 402 66 402 76C402 112 477 416 492 473Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="162.727294921875" overflow="visible" y="327.7272720336914" height="9" width="9.443181991577148"><ns0:polyline points="0.00,8.06 4.72,4.91 9.44,8.06" style="fill:none;fill-opacity:1;stroke-width:1px;stroke:rgb(0,0,0);stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g></ns0:svg></ns0:svg>
Now, the length of the projection of $\overrightarrow{a}$ on $\overrightarrow{u}$ is $|\overrightarrow{a}|\cos \theta$. We can scale the unit vector $\hat{u}$ (along $\overrightarrow{u}$) by this amount to get $$\vec{a}{||} = \hat{u}(|\vec{a}|\cos \theta) $$
But, $\overrightarrow{a}\cdot \overrightarrow{u}=|\overrightarrow{a}||\overrightarrow{u}|\cos \theta$, and $\hat{u}=\frac{\overrightarrow{u}}{|\overrightarrow{u}|}$. Puting it all together, we get $$\vec{a} = \frac{{\vec{a} \cdot \vec{u}}}{|\vec{u}|^2}$$

<ns0:svg xmlns:ns0="http://www.w3.org/2000/svg" x="0" y="0" width="661.45458984375" height="459.90911865234375" style=" width:661.45458984375px; height:459.90911865234375px; background: transparent; fill: none; "> <ns0:svg class="role-diagram-draw-area"><ns0:g class="shapes-region" style="stroke: black; fill: none;"><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L586.82,260" style="stroke: rgb(0, 0, 0); stroke-width: 2; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-1,1.2246467991473532e-16,-1.2246467991473532e-16,-1,589.8181762695312,260.00000000000006)" style="stroke: rgb(0, 0, 0); stroke-width: 2;"><ns0:path d=" M14.21,-4.28 Q6.45,-0.59 0,0 Q6.45,0.59 14.21,4.28" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L109.39,427.61" style="stroke: rgb(0, 0, 0); stroke-width: 2; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(0.7071067811865474,-0.7071067811865477,0.7071067811865477,0.7071067811865474,107.2727279663086,429.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 2;"><ns0:path d=" M14.21,-4.28 Q6.45,-0.59 0,0 Q6.45,0.59 14.21,4.28" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L277,36.73" style="stroke: rgb(0, 0, 0); stroke-width: 2; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(3.061616997868383e-16,1,-1,3.061616997868383e-16,277,33.727272033691406)" style="stroke: rgb(0, 0, 0); stroke-width: 2;"><ns0:path d=" M14.21,-4.28 Q6.45,-0.59 0,0 Q6.45,0.59 14.21,4.28" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L291.2,350.78" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.15453795241861665,-0.9879868527780424,0.9879868527780424,-0.15453795241861665,291.81817626953125,354.72727203369135)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M291.82,354.73 L438.08,398.99" style="stroke: rgb(29, 34, 46); stroke-width: 5; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(29,34,46)" transform="matrix(-0.957117481995526,-0.28970006154390765,0.28970006154390765,-0.957117481995526,443.81817626953125,400.7272720336914)" style="stroke: rgb(29, 34, 46); stroke-width: 5;" stroke-opacity="1"><ns0:path d=" M25.14,-7.57 Q11.41,-1.03 0,0 Q11.41,1.03 25.14,7.57" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L423.26,304.26" style="stroke: rgb(29, 34, 46); stroke-width: 5; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(29,34,46)" transform="matrix(-0.957117481995526,-0.28970006154390765,0.28970006154390765,-0.957117481995526,429,306)" style="stroke: rgb(29, 34, 46); stroke-width: 5;" stroke-opacity="1"><ns0:path d=" M25.14,-7.57 Q11.41,-1.03 0,0 Q11.41,1.03 25.14,7.57" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M429,306 L443.2,396.78" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.15453795241861665,-0.9879868527780424,0.9879868527780424,-0.15453795241861665,443.81817626953125,400.72727203369135)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L442.29,399.44" style="stroke: rgb(0, 0, 0); stroke-width: 1; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.7643590058228539,-0.6447909042608297,0.6447909042608297,-0.7643590058228539,443.8181762695313,400.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 1;"><ns0:path d=" M10.93,-3.29 Q4.96,-0.45 0,0 Q4.96,0.45 10.93,3.29" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M277,260 L346.74,190.26" style="stroke: rgb(52, 61, 85); stroke-width: 4; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(52,61,85)" transform="matrix(-0.7071067811865479,0.7071067811865471,-0.7071067811865471,-0.7071067811865479,350.2727279663086,186.7272720336914)" style="stroke: rgb(52, 61, 85); stroke-width: 4;" stroke-opacity="1"><ns0:path d=" M20.77,-6.25 Q9.42,-0.85 0,0 Q9.42,0.86 20.77,6.25" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M349,188 L363.2,278.78" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.15453795241861665,-0.9879868527780424,0.9879868527780424,-0.15453795241861665,363.81817626953125,282.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M363.82,282.73 L510.08,326.99" style="stroke: rgb(29, 34, 46); stroke-width: 5; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(29,34,46)" transform="matrix(-0.957117481995526,-0.28970006154390765,0.28970006154390765,-0.957117481995526,515.8181762695312,328.7272720336914)" style="stroke: rgb(29, 34, 46); stroke-width: 5;" stroke-opacity="1"><ns0:path d=" M25.14,-7.57 Q11.41,-1.03 0,0 Q11.41,1.03 25.14,7.57" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M349,188 L495.26,232.26" style="stroke: rgb(29, 34, 46); stroke-width: 5; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(29,34,46)" transform="matrix(-0.957117481995526,-0.28970006154390765,0.28970006154390765,-0.957117481995526,501,234)" style="stroke: rgb(29, 34, 46); stroke-width: 5;" stroke-opacity="1"><ns0:path d=" M25.14,-7.57 Q11.41,-1.03 0,0 Q11.41,1.03 25.14,7.57" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M501,234 L515.2,324.78" style="stroke: rgb(0, 0, 0); stroke-width: 3; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.15453795241861665,-0.9879868527780424,0.9879868527780424,-0.15453795241861665,515.8181762695312,328.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 3;"><ns0:path d=" M17.49,-5.26 Q7.94,-0.72 0,0 Q7.94,0.72 17.49,5.26" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M349,188 L514.29,327.44" style="stroke: rgb(0, 0, 0); stroke-width: 1; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(-0.7643590058228539,-0.6447909042608297,0.6447909042608297,-0.7643590058228539,515.8181762695312,328.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 1;"><ns0:path d=" M10.93,-3.29 Q4.96,-0.45 0,0 Q4.96,0.45 10.93,3.29" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M429,306 L498.74,236.26" style="stroke: rgb(52, 61, 85); stroke-width: 4; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(52,61,85)" transform="matrix(-0.7071067811865479,0.7071067811865471,-0.7071067811865471,-0.7071067811865479,502.2727279663086,232.7272720336914)" style="stroke: rgb(52, 61, 85); stroke-width: 4;" stroke-opacity="1"><ns0:path d=" M20.77,-6.25 Q9.42,-0.85 0,0 Q9.42,0.86 20.77,6.25" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M443.82,400.73 L513.56,330.99" style="stroke: rgb(52, 61, 85); stroke-width: 4; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(52,61,85)" transform="matrix(-0.7071067811865479,0.7071067811865471,-0.7071067811865471,-0.7071067811865479,517.09090423584,327.4545440673828)" style="stroke: rgb(52, 61, 85); stroke-width: 4;" stroke-opacity="1"><ns0:path d=" M20.77,-6.25 Q9.42,-0.85 0,0 Q9.42,0.86 20.77,6.25" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M291.82,354.73 L361.56,284.99" style="stroke: rgb(52, 61, 85); stroke-width: 4; fill: none; fill-opacity: 1; stroke-opacity: 1;" /><ns0:g stroke="rgb(52,61,85)" transform="matrix(-0.7071067811865479,0.7071067811865471,-0.7071067811865471,-0.7071067811865479,365.09090423583984,281.4545440673828)" style="stroke: rgb(52, 61, 85); stroke-width: 4;" stroke-opacity="1"><ns0:path d=" M20.77,-6.25 Q9.42,-0.85 0,0 Q9.42,0.86 20.77,6.25" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M284.41,307.36 C309.31,299.88 313.65,284.36 295.93,263.98" style="stroke: rgb(0, 0, 0); stroke-width: 1; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(0.6709444523936378,0.7415076141228771,-0.7415076141228771,0.6709444523936378,294.81817626953125,262.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 1;"><ns0:path d=" M10.93,-3.29 Q4.96,-0.45 0,0 Q4.96,0.45 10.93,3.29" /></ns0:g></ns0:g><ns0:g class="arrow-line"><ns0:path class="connection real" stroke-dasharray="" d=" M303.41,280.36 C325.37,262.1 325.81,253.09 307.94,232.97" style="stroke: rgb(0, 0, 0); stroke-width: 1; fill: none; fill-opacity: 1;" /><ns0:g stroke="#11111b" transform="matrix(0.6709444523936378,0.7415076141228771,-0.7415076141228771,0.6709444523936378,306.81817626953125,231.7272720336914)" style="stroke: rgb(0, 0, 0); stroke-width: 1;"><ns0:path d=" M10.93,-3.29 Q4.96,-0.45 0,0 Q4.96,0.45 10.93,3.29" /></ns0:g></ns0:g><ns0:g /></ns0:g><ns0:g /><ns0:g /><ns0:g /></ns0:svg> <ns0:svg width="660" height="458.4545593261719" style="width:660px;height:458.4545593261719px;font-family:Asana-Math, Asana;background:transparent;">ns0:g<ns0:g /></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,271.20458984375,357.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M271 204L242 77C238 60 236 42 236 26C236 4 245 -9 260 -9C283 -9 324 17 406 85L399 106C375 86 346 59 324 59C315 59 309 68 309 82C309 87 309 90 310 93L402 472L392 481L359 463C318 478 301 482 274 482C246 482 226 477 199 464C137 433 104 403 79 354C35 265 4 145 4 67C4 23 19 -11 38 -11C75 -11 155 41 271 204ZM319 414C297 305 278 253 244 201C187 117 126 59 94 59C82 59 76 72 76 99C76 163 104 280 139 360C163 415 186 433 234 433C257 433 275 429 319 414Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="270.727294921875" overflow="visible" y="338.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,322.52276611328125,175.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M342 330L365 330C373 395 380 432 389 458C365 473 330 482 293 482C248 483 175 463 118 400C64 352 25 241 25 136C25 40 67 -11 147 -11C201 -11 249 9 304 54L354 95L346 115L331 105C259 57 221 40 186 40C130 40 101 80 101 159C101 267 136 371 185 409C206 425 230 433 261 433C306 433 342 414 342 390Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="321.727294921875" overflow="visible" y="156.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:gns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,411.04547119140625,336.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M235 722L223 733C171 707 135 698 63 691L59 670L107 670C131 670 141 663 141 646C141 639 140 628 139 622L38 71C37 68 37 64 37 61C37 22 85 -11 140 -11C177 -11 228 8 271 39C367 107 433 244 433 376C433 414 424 453 412 468C405 477 392 482 377 482C353 482 323 474 295 460C244 433 211 403 149 324ZM322 424C348 424 361 401 361 352C361 288 340 202 310 137C277 68 237 36 183 36C137 36 112 59 112 101C112 135 127 276 208 361C241 395 293 424 322 424Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g><ns0:svg x="410.727294921875" overflow="visible" y="313.7272720336914" height="10" width="9.340909004211426"><ns0:path d=" M 9.34 4.85 l -3.15 -3.32 l -0.49 0.52 l 1.93 2.33 h -0.15 v 0.90 h 0.15 l -1.93 2.33 l 0.49 0.52 z M 1.68 5.23 h 7.20 v -0.90 h -7.20 z" style="fill:rgb(0,0,0);fill-opacity:1;stroke-width:1px;stroke:none;stroke-opacity:1;" /></ns0:svg></ns0:g></ns0:g></ns0:g>ns0:g<ns0:g /></ns0:g>ns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,301.727294921875,321.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M237 -16C473 -16 572 316 576 504C578 618 546 702 419 702C159 702 72 412 69 199C67 80 101 -16 237 -16ZM401 676C536 676 506 491 485 381L169 381C194 485 272 676 401 676ZM253 13C102 13 147 261 163 349L479 349C454 237 396 13 253 13Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g>ns0:gns0:gns0:g<ns0:g transform="matrix(1,0,0,1,326.727294921875,239.7272720336914)"><ns0:path transform="matrix(0.017,0,0,-0.017,0,0)" d="M622 285C624 428 505 474 382 473C398 548 407 624 432 699L432 705C418 700 404 693 389 684L354 473C184 474 30 367 27 185C24 37 142 -8 268 -16L229 -289C249 -282 267 -274 282 -261C283 -179 288 -98 299 -16C481 -3 618 87 622 285ZM539 273C537 130 451 11 301 6L377 449C487 447 541 380 539 273ZM349 449L270 5C155 14 106 73 108 187C111 336 196 444 349 449Z" stroke="rgb(0,0,0)" stroke-opacity="1" stroke-width="8" fill="rgb(0,0,0)" fill-opacity="1" /></ns0:g></ns0:g></ns0:g></ns0:g></ns0:svg></ns0:svg>

for the paralellogram formed by $\overrightarrow{a}$ and $\overrightarrow{b}$ the area is $|\overrightarrow{a}||\overrightarrow{b}|\sin \theta$. we know that $cos\theta =\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$. Putting in together, the area of the paralellogram $A$ is given by: $$ A^2 = |\vec{a}|^2|\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$$
Allowing $a,b\in {\mathbb{R}}^2$, $\overrightarrow{a}=\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$, $\overrightarrow{b}=\left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]$.
we have $$ A = a_{1}b_{2} - a_{2}b_{1}$$
This expression is commonly given as a determinant $$A = \begin{vmatrix}
a_{1} \ a_{2} \
b_{1} \ b_{2}
\end{vmatrix} $$

Similarly, in ${\mathbb{R}}^3$, if $\overrightarrow{a}=\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]$, $\overrightarrow{b}=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]$, $\overrightarrow{c}=\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\end{array}\right]$

Then, the area of the parallelopiped is given by $$\begin{vmatrix}
a_{1} \ a_{2} \ a_{3} \
b_{1} \ b_{2} \ b_{3} \
c_{1} \ c_{2 } \ c_{3}
\end{vmatrix} = a_{1}\begin{vmatrix}
b_{2} \ b_{3} \
c_{2} \ c_{3}
\end{vmatrix} - a_{2}\begin{vmatrix}
b_{1} \ b_{3} \
c_{1} \ c_{3}
\end{vmatrix} + a_{3}\begin{vmatrix}
b_{1} \ b_{2} \
c_{1} \ c_{2}
\end{vmatrix}$$

we will not PROVE THIS FACT.

Cross product in ${\mathbb{R}}^3$:

again revisiting the discussion of the area of a parallelogram, only this time in 3d space:
for the parallelogram formed by $\overrightarrow{a}$ and $\overrightarrow{b}$ the area is $|\overrightarrow{a}||\overrightarrow{b}|\sin \theta$. we know that $cos\theta =\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$. Putting in together, the area of the parallelogram $A$ is given by: $$ A^2 = |\vec{a}|^2|\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$$
letting $\overrightarrow{a},\overrightarrow{b}\in {\mathbb{R}}^3$ we obtain that $$A = \sqrt{ (a_{1}b_{2} - a_{2}b_{1})^2 + (a_{2}b_{3} -a_{3}b_{2})^2 +(a_{1}b_{3}-a_{3}b_{1})^2 }$$
Now, notice A = $|\overrightarrow{a}\times \overrightarrow{b}|$ as computing the determinant gives us $$\vec{a} \times \vec{b} = \begin{bmatrix}
a_{1}\a_{2}\a_{3}
\end{bmatrix}\times \begin{bmatrix}
b_{1} \ b_{2} \ b_{3}
\end{bmatrix}= \begin{vmatrix}
i \ \ \ j \ \ \ k \
a_{1} \ a_{2} \ a_{3} \
b_{1} \ b_{2} \ b_{3}
\end{vmatrix} = (a_{1}b_{2} - a_{2}b_{1})i + (a_{2}b_{3} -a_{3}b_{2})j +(a_{1}b_{3}-a_{3}b_{1})k $$

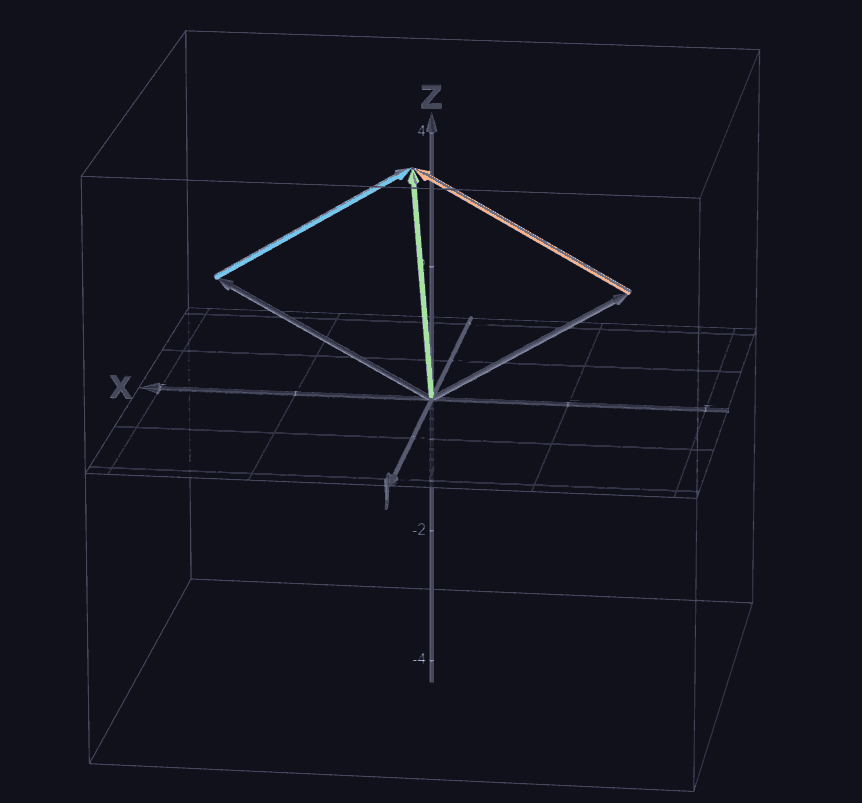
Now, here is the the cool thing, intuitively, we know that two vectors in ${\mathbb{R}}^3$ specify a plane.

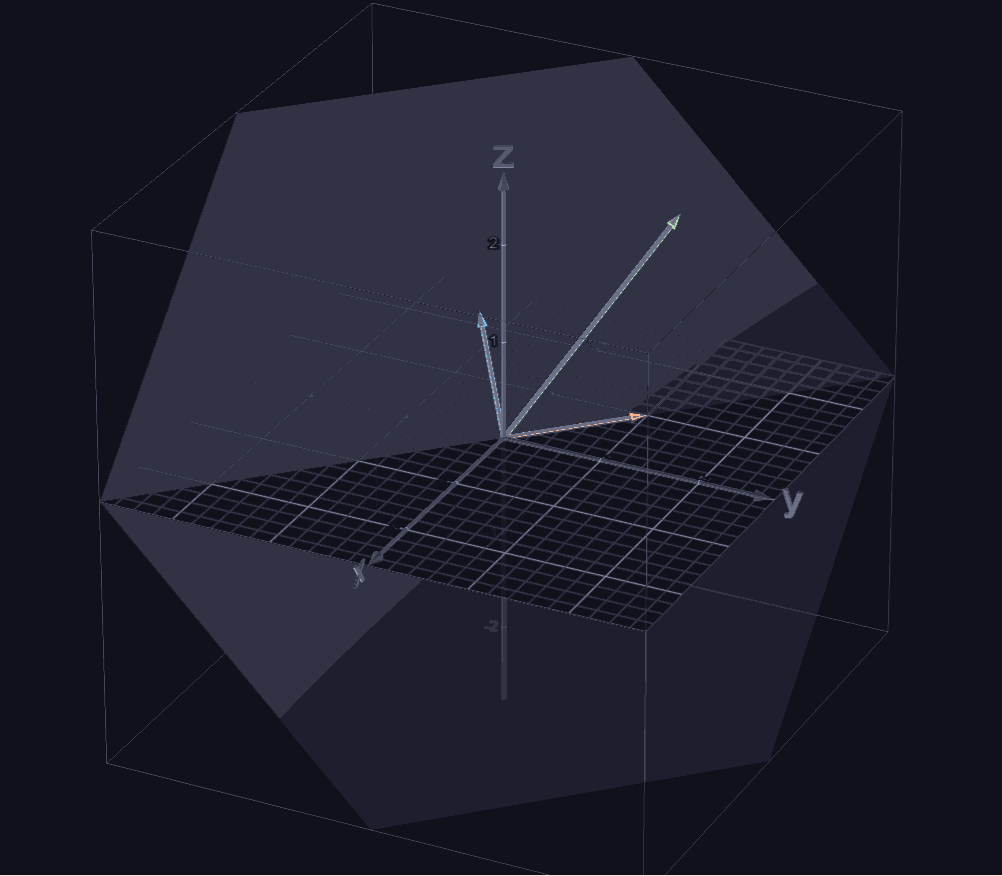
Notice that if $\overrightarrow{x}=[x_1,x_2,x_3{]}^T$ (I don't like writing column vectors anymore haha so I will do row transpose)
is on the plane of the vectors $\overrightarrow{a},\overrightarrow{b}$ (both tails attached to the origin) then from the picture above, it must be that there exists scalars $\lambda ,\mu$ such that $\lambda \overrightarrow{a}+\mu \overrightarrow{b}=\overrightarrow{x}$ that is, for every point $\overrightarrow{x}$ on this plane, we can scale $\overrightarrow{a},\overrightarrow{b}$ to complete the parallelogram. Then we have the set of equations as follows:

Using any two equations, and solving for the scalars, and using the third, we get

but notice the coefficients are actually the co-ordinates of $\overrightarrow{a}\times \overrightarrow{b}$.
In particular, The plane formed by the vectors $\overrightarrow{a},\overrightarrow{b}$ is given by $(\overrightarrow{a}\times \overrightarrow{b})\cdot \overrightarrow{x}=\overrightarrow{0}$. That is that the cross product of two vectors in ${\mathbb{R}}^3$ is perpendicular or orthogonal to the plane formed by those vectors.