1 - logic gates

Binary logic gate

let $B = {0, 1}$ . any function $f : B^{2} \to B$ is called a binary logic gate.

$B^{2}$ contains $4$ tuples, and each of these tuples can be assigned one of two outputs, to uniquely determine a binary logic gate. Hence there are $16$ binary logic gates.
We will denote binary logic gates as $B F$
These are also called Boolean functions

In the picture below, we have all 16 possible binary logic gates, and their co-responding (continuous and differentiable) real valued analogs.
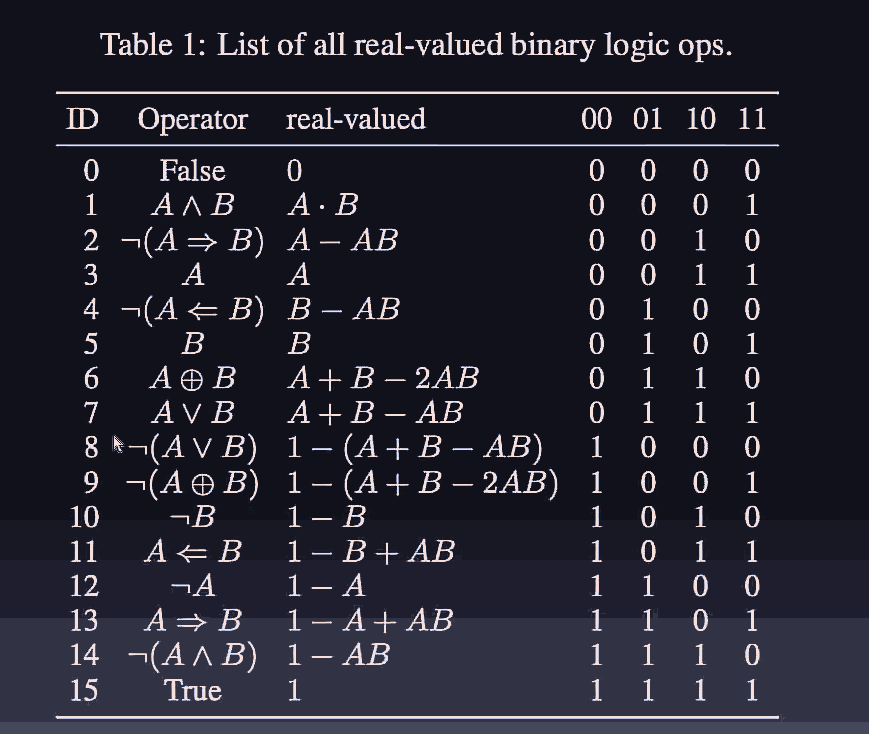
Support/Figures/Pasted image 20250108221755.png
Remember that $A ⟹ B$ is true if: $A$ is false, or $A, B$ are both true. In particular, $A ⟹ B$ is equivalent to $\neg A \lor B$ .

logic gate composition

A logic gate composition graph is a directed acyclic graph (DAG) $G$ where:

The nodes of $G$ are either binary variables $A, B \in {0, 1}$ or instances of logic gates.
An edge $(u, v)$ exists if and only if $v$ is an instance of a logic gate, and $u$ is either a binary variable or the output of another logic gate instance.
Each logic gate instance in the graph has an indegree of exactly two, meaning it takes exactly two inputs.
Each logic gate instance has an outdegree of exactly one, meaning it produces a single output.

It is clear that all 16 logic gates can be written as a composition of $A N D, O R, N O T$ .

universal logic gates

A function $f \in B F$ is universal if for every $g \in B F$ and every $A, B \in {0, 1}$ , there exists a logic gate composition $G$ whose nodes are $A$ , $B$ , or instances of $f$ , such that the function modelled by this graph is $g$ .

$N A N D$ is a universal logic gate. So is $N O R$ . For example it is sufficient to show that $A N D, O R, N O T$ can be modelled from $N A N D$
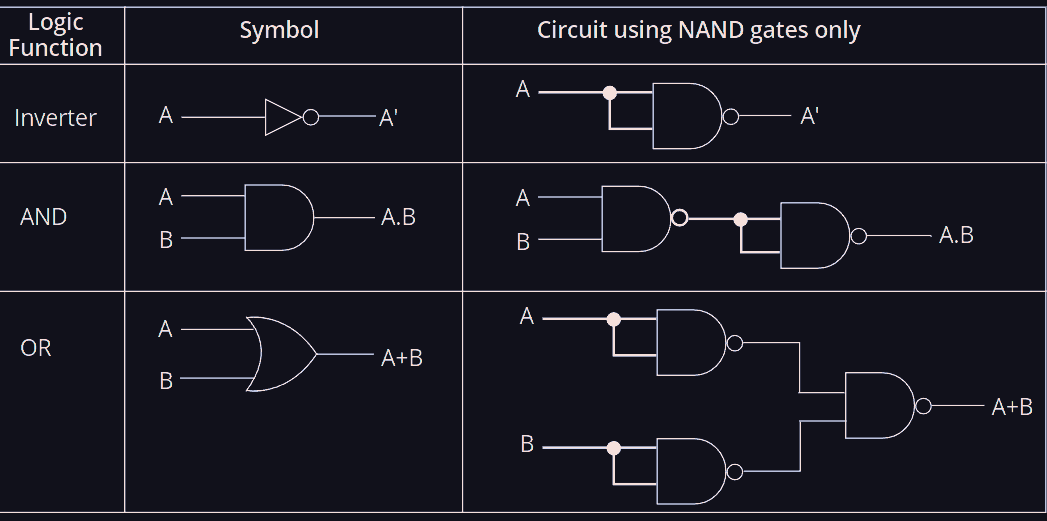
Support/Figures/Pasted image 20250108225213.png

The paper uses all 16 logic gates (their real analog) and don't use universal gates to model