A function is generically written $x\mapsto f(x)$. With the same map $f$, $y\mapsto f(y)$, is $\alpha$-equivalent to $x\mapsto f(x)$. the process of substituting $x$ with $y$ is called $\alpha$-substitution.

The same function can be written $\lambda x\cdot f(x)$.
to apply a function, we need to substitute $x$ with something, and evaluate, which we call $\beta$ reduction.
for example, $(\lambda x.x+1)3{\to }_{\beta }3+1$.

In general if a lambda expression maps $x$ to $M$ (which is M(x)), written $\lambda x.M$, it's $\beta$-reduction with some value $a$ is written $\lambda x.M{\to }_{\beta }M[x/a]$, where the slash denotes that $a$ is substitute for $x$.

This is a complete programming language, called lambda calculus. We can define variables, which can themselves be functions, and the output of functions can also be functions.

Suppose we wanted to capture the map $(x,y)\mapsto (x+y)$. Well, let's write an abstract two variable function. consider $\lambda x.\lambda y.M$ where $M$ is a function of $(x,y)$. then for a pair of inputs $a,b$, we have the following $\beta$-reductions:

Notice we do substitutions from left to right. This method is called currying.

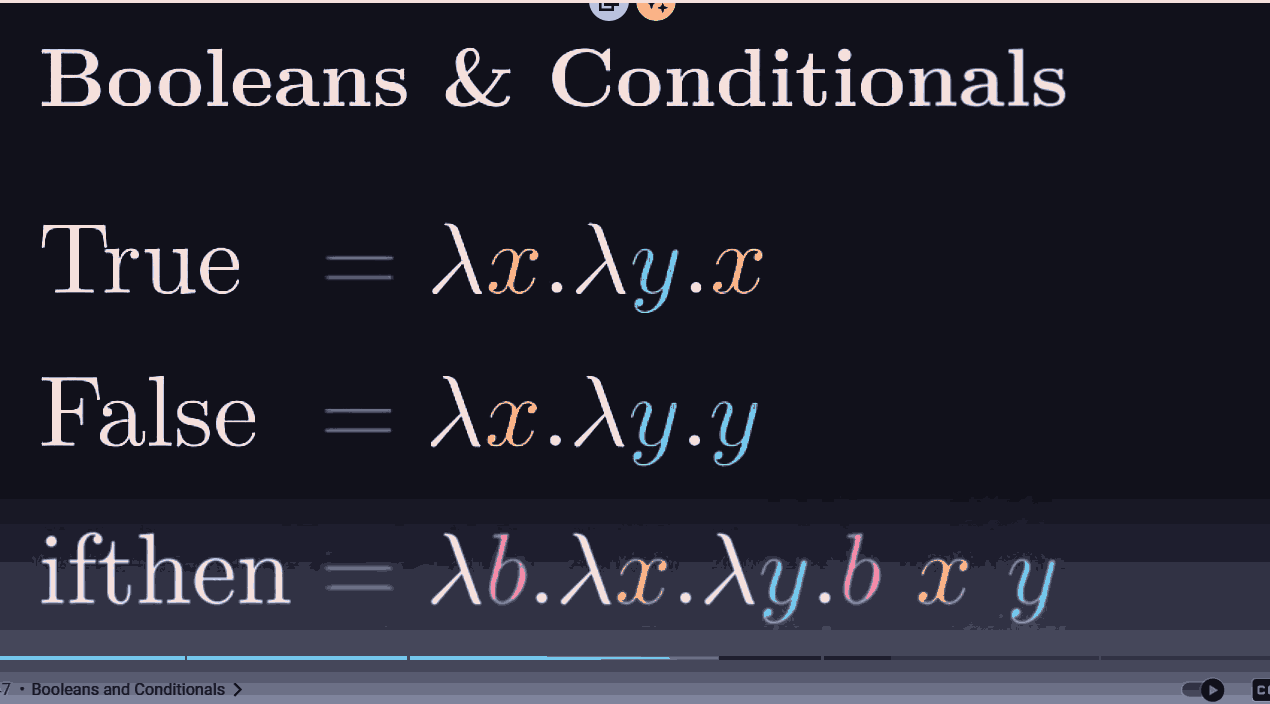
Given two things, True returns the first thing, and false returns the second thing, this encoding works, and one can check it by plugging in True and False for b in the if then. (True and False are functions here as specified in the picture)

Basically, we need to enforce types on the inputs.

Curry - Howard Co-respondence

We can write proofs in simply typed lambda calculus in the following way. suppose A,B are types, then we can think of A and B as propositions. A is true if there exists a variable $x$ of type $A$. (similarly for B).

Now, the implication $A=>B$, is equivalent to some function that takes $A\to B$. We can map the argument $A$ is true, $A⟹B$ is true, hence $B$ is true to the following lambda calculus statement:
$\mathrm{\exists }a\in A,\mathrm{\exists }\lambda x.M,M(x)\in B$, hence $M(a)\in B$ (in other words $B$ is true).

Lambda Calculus Re-write Rules

Lambda calculus is based on a few key re-write rules that help simplify and manipulate lambda expressions. These include beta reduction, alpha conversion, and eta conversion.

1. Beta Reduction (Application)

Beta reduction is the most important re-write rule. It describes how a function (lambda expression) is applied to an argument, by substituting the argument for the function's parameter.

• Explanation:
  • $(\lambda x.E)$ is a lambda expression (a function) where $x$ is the parameter and $E$ is the body of the function.
  • $A$ is the argument applied to the function.
  • The result is the body $E$ with $x$ replaced by $A$, denoted as $E[x:=A]$ (substituting $x$ with $A$ in $E$).

Example:

2. Alpha Conversion (Renaming Variables)

Alpha conversion allows renaming of bound variables (variables within the scope of a lambda) to avoid conflicts. It is used to change the name of the bound variable in a lambda expression.

• Explanation:
  • You can rename the bound variable $x$ to another variable $y$ as long as $y$ is not already used in $E$.

Example:

3. Eta Conversion (Simplifying Functions)

Eta conversion simplifies functions that return another function. It allows you to remove unnecessary function abstractions.

• Explanation:
  • If a function $\lambda x.(Fx)$ applies $F$ to $x$ and $x$ does not appear free in $F$, the function can be simplified to $F$.

Example: