Hyperparameter Tuning - 2

Min batch grad descent

let $X,Y$ be the training set. Split it into mini batches $X^t,Y^t$ with batch size $B$, where $0\le t\le m/B$ (taken to the nearest integer).
One epoch of a neural network training cycle is one forward and one backward pass, with one update step. let the number of batches be $H=m/B$. Then one epoch of min-batch-gradient descent would look like:

for t from 0 to H: 
	forwardPropogation(Xt,Yt)
	backwardPropogation(Xt,Yt)
	UpdateParameters(Xt,Yt)

so one epoch involves doing a forward, backward and update pass on each batch. we may do multiple epochs to finish the training process.

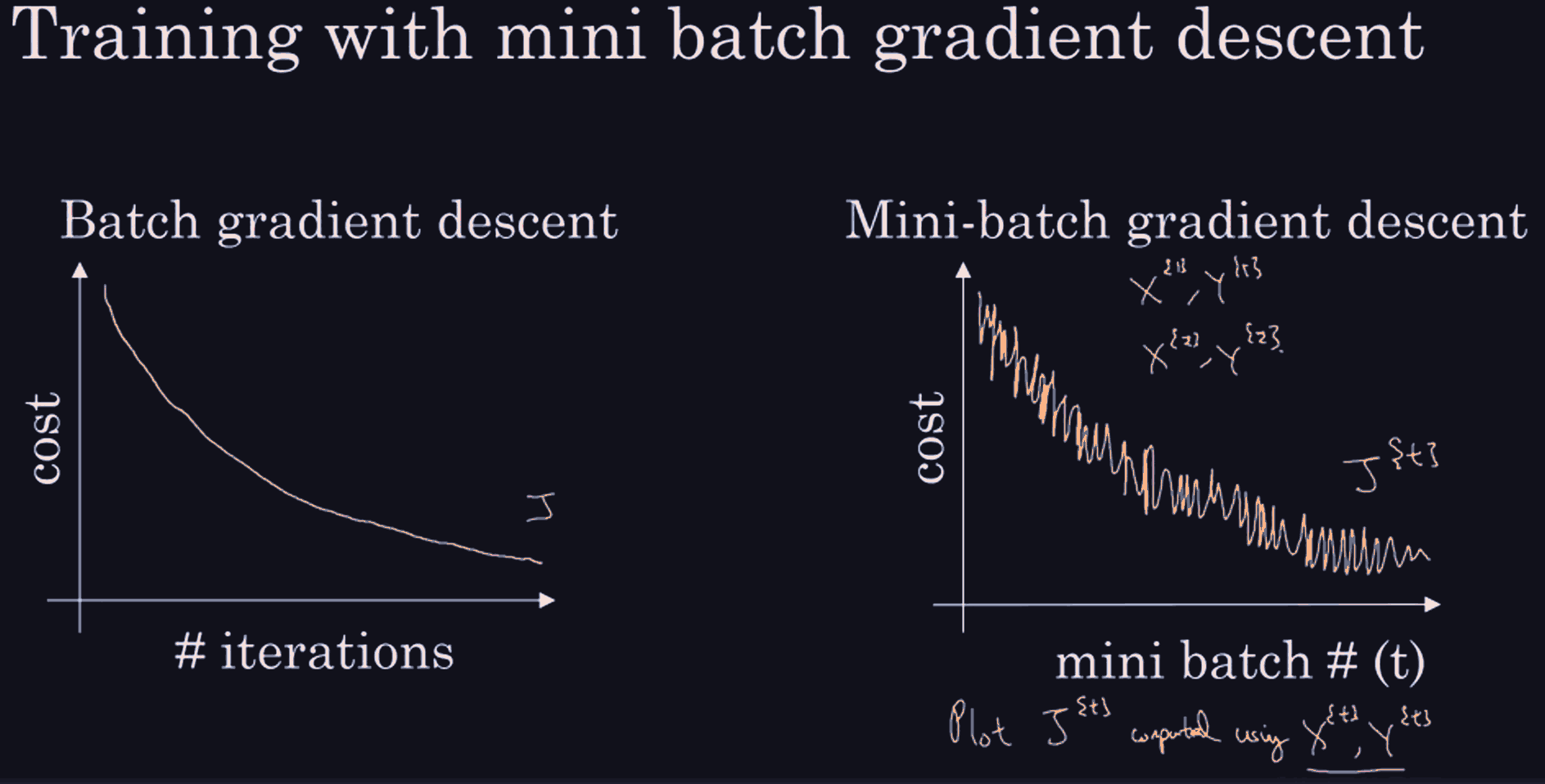
The idea here is that in one epoch, the moment we go from one batch to another, our cost might rise. and then doing the backprop and update on the new batch will get it down again, hence the oscillations in the right-hand graph.
if the batch size $H=m$, then we just have normal single batch gradient descent.
if the batch size $H=1$, so each epoch involves gradient descent on each example individually. (called stochastic gradient descent)

purple: stochastic gradient descent, blue: single batch gradient descent.
with stochastic gradient descent, although you make progress towards the minimum with every example, you do lose the speed you gained because there is no vectorization.
With single batch gradient descent, each iteration can be very slow even after vectorization if the datasets are large AF. So somewhere in between is the sweet spot. where each batch size is large enough to take advantage of vectorization, and small enough so that each batch pass isn't too slow, and we make progress towards the minimum quickly.